2025 Senior Q2

Q2 of this year’s S(ingapore)MO Senior Round 2 was my proposal (so is Q3 but that one isn’t very interesting), and I just wanted to share a little about the problem development process.

The problem as screenshotted from AoPS

The diagram as screenshotted from GeoGebra

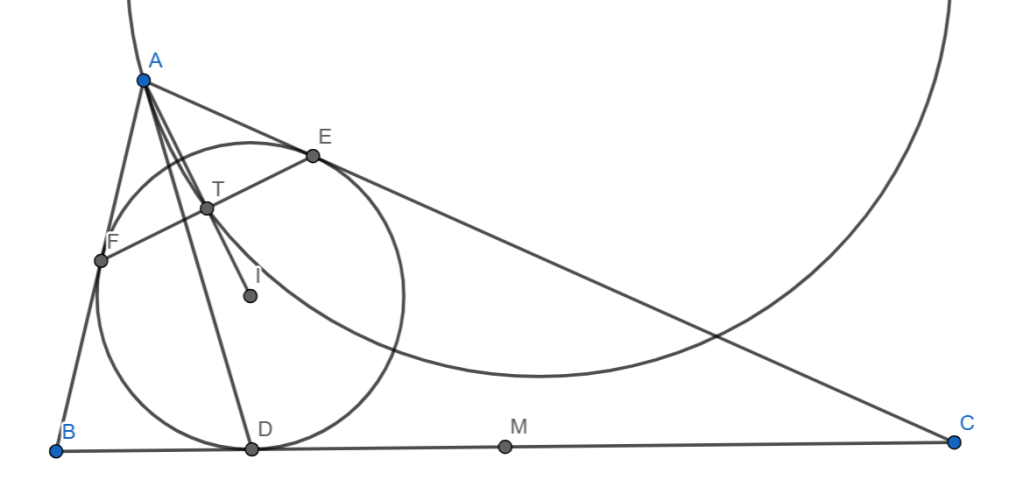
First let me talk about how to draw an accurate diagram. If we let $E$ and $F$ be the other 2 intouch points, and $T$ be the midpoint of $EF$ (see diagram below), then $IT\times IA=IE^2=IX^2$ , hence $T$ lies on $(AXY)$ . We can thus uniquely determine the center $O$ using

The perpendicular from $A$ to $AD$ and
The perpendicular bisector of $AT$ .

Anyways. One day I was looking at a geom solution that involves radius zero circles, and I thought it would be fun to try and construct a problem with the idea.¹ For those who are unfamiliar with the technique, you can read this handout.

So what I wanted was a midpoint on a nice collinearity. Why?

If say $M$ is the midpoint of $AA'$ and also lies on line $BB'$ , then we can find a circle tangent to $AA'$ at $A$ for which $M-B-B'$ is the radical axis of this circle and the radius zero circle $A'$ . To make the problem work, $M$ has to be a less well-known point so I can conceal it.

With that in mind, I started scrolling through this handout until I saw this config:

In particular, the line $N_2 - I - M$ . This is true because it is the midline of $A-D'-X$ , a classic collinearity.

As discussed above, there exists a circle tangent to $AD$ at $A$ such that $IM$ is the radical axis of this circle and $(D)$ . What exactly is this circle? Currently, I only had one condition: that it was tangent to $AD$ at $A$ . So, I needed to find one more point on the circle.

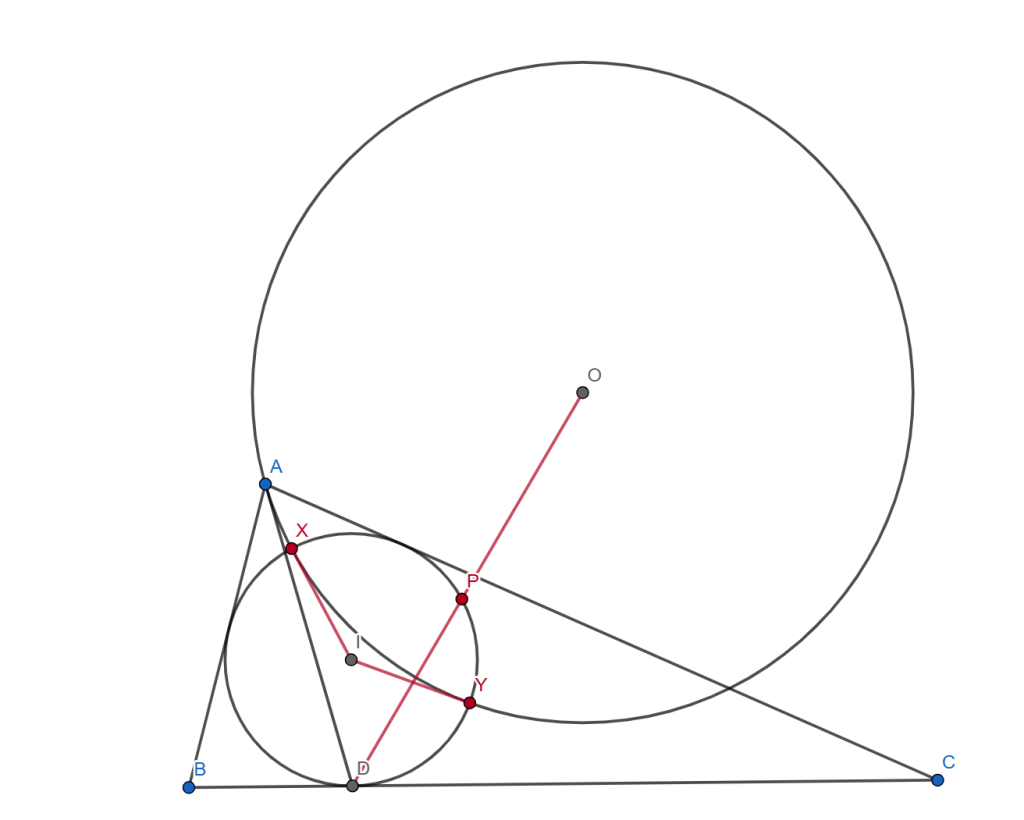
Since $I$ is on the radical axis, the power from $I$ to the circle is $ID^2$ , and so $IX,IY$ are tangent to the circle. (This is the $X,Y$ in the original question.)

This means the two circles are orthogonal. Hence, if I marked the point $P$ where $DO$ intersects the incircle, $OA^2=OP\times OD$ , and hence $\angle OPD=90^\circ$ .

But we know many properties of $P$ – for example, it passes through the point diametrically opposite $D$ on the incircle, and also passes through the extouch.

If we look at this classic problem, we are motivated to construct the circle through $M$ with radius $MD$ . So I put all of that in a diagram:

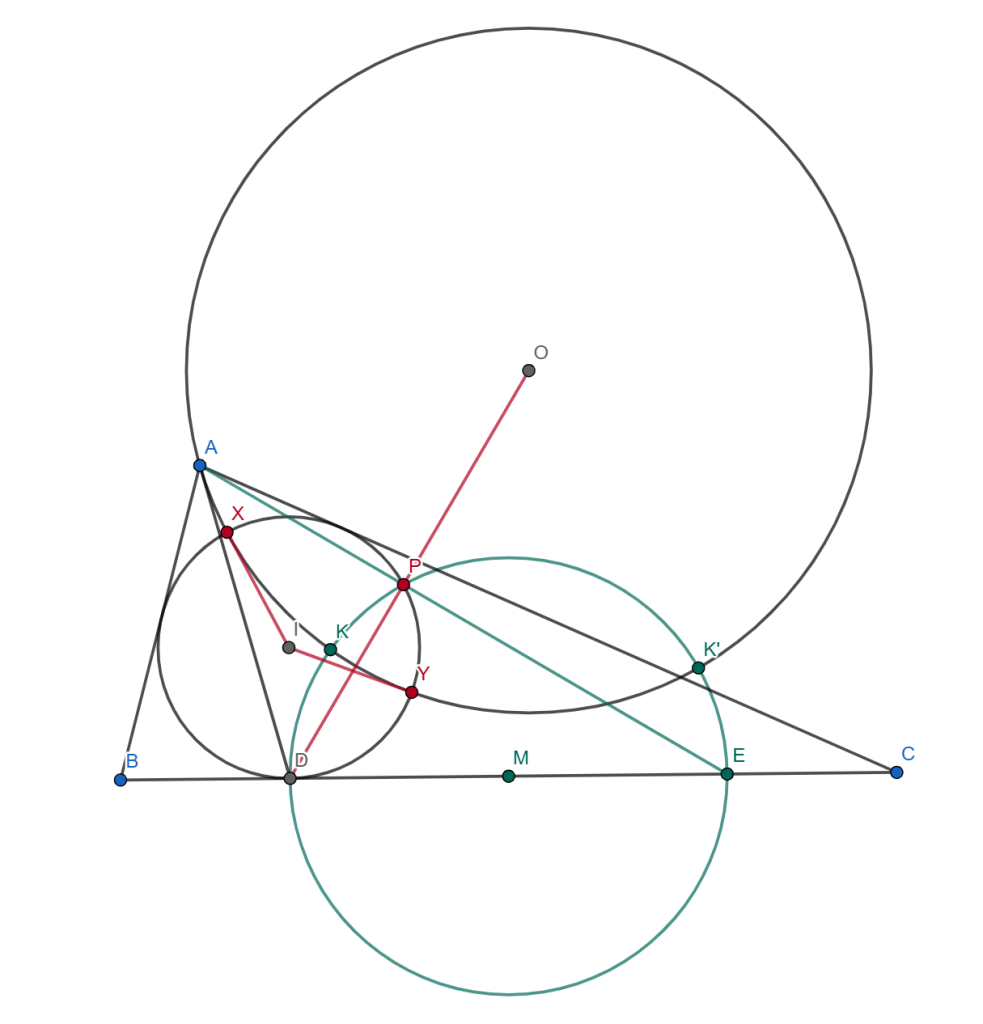
At this point, I had three mutually orthogonal circles. This gave me new ways to define $(AXY)$ . For example $X,Y,M$ are collinear and $K',K,I$ are also collinear.

I knew there was a proposal somewhere in this diagram already, and I just had to find what i wanted to ask. There were a lot of possible questions, and I tried to find the one that defines the least number of points.

I forgot exactly what I tried here, but I eventually ended up with the following which I was satisfied with:

Let $I$ be the incenter of $\triangle ABC$ and $\omega$ be its incircle. Let $D$ be the intersection of $\omega$ with $BC$ . Suppose $X,Y$ are points on $\omega$ such that $XY$ bisects $BC$ and $AD$ is tangent to the circumcircle of $\triangle AXY$ . Prove that $IX$ and $IY$ are also tangent to the circumcircle of $\triangle AXY$ .

While lying in bed, I realised that I could combine all the tangencies into one condition and ask to prove $XY$ bisects $BC$ instead, and that’s how I ended up with the actual question. As a bonus, this version had a zero radius circle solution too.

I passed this question to a bunch of other X-men to testsolve, and the consensus is that it was roughly a easy Q2 level question.

So I submitted it, and to my surprise it really ended up as a Q2.

If we go back one step further, the reason why I was thinking about constructing geom problems at all is because of the quality of geom problems at SMO last year. ↩︎

2025 Senior Q2

Comments

Leave a comment Cancel reply